Let the Random Variable X Represent the Number of Girls in a Family

four.2 Probability Distributions for Discrete Random Variables

Learning Objectives

1. To learn the concept of the probability distribution of a discrete random variable.
2. To learn the concepts of the mean, variance, and standard deviation of a discrete random variable, and how to compute them.

Probability Distributions

Associated to each possible value x of a discrete random variable X is the probability $P\left(\mathrm{ten}\right)$ that X volition take the value x in one trial of the experiment.

Definition

The probability distributionA list of each possible value and its probability. of a discrete random variable X is a list of each possible value of X together with the probability that X takes that value in one trial of the experiment.

The probabilities in the probability distribution of a random variable X must satisfy the following ii conditions:

1. Each probability $P\left(x\right)$ must be between 0 and 1: $0\le P\left(\mathrm{10}\right)\le 1.$
2. The sum of all the probabilities is ane: ${\displaystyle \mathrm{\Sigma }P\left(x\right)=1}.$

Instance 1

A fair coin is tossed twice. Allow X exist the number of heads that are observed.

1. Construct the probability distribution of X.
2. Detect the probability that at least ane head is observed.

Solution:

1. The possible values that X can accept are 0, 1, and 2. Each of these numbers corresponds to an event in the sample infinite $S=\left\{hh,ht,th,tt\right\}$ of equally likely outcomes for this experiment: X = 0 to $\left\{tt\right\}$ , X = one to $\left\{ht,th\right\}$ , and X = 2 to $\left\{hh\right\}.$ The probability of each of these events, hence of the corresponding value of X, tin can be institute simply past counting, to give

   $$\begin{array}{cccc}\mathrm{10}& 0& \mathrm{ane}& \mathrm{ii}\\ P\left(x\right)& 0.25& 0.50& 0.25\end{array}$$

   This table is the probability distribution of X.

2. "At least one head" is the event 10 ≥ 1, which is the union of the mutually exclusive events X = 1 and X = 2. Thus

   $$P\left(\mathrm{10}\ge 1\right)=P\left(\mathrm{one}\right)+P\left(2\right)=0.50+0.25=0.75$$

   A histogram that graphically illustrates the probability distribution is given in Figure 4.i "Probability Distribution for Tossing a Off-white Coin Twice".

Figure 4.ane Probability Distribution for Tossing a Fair Coin Twice

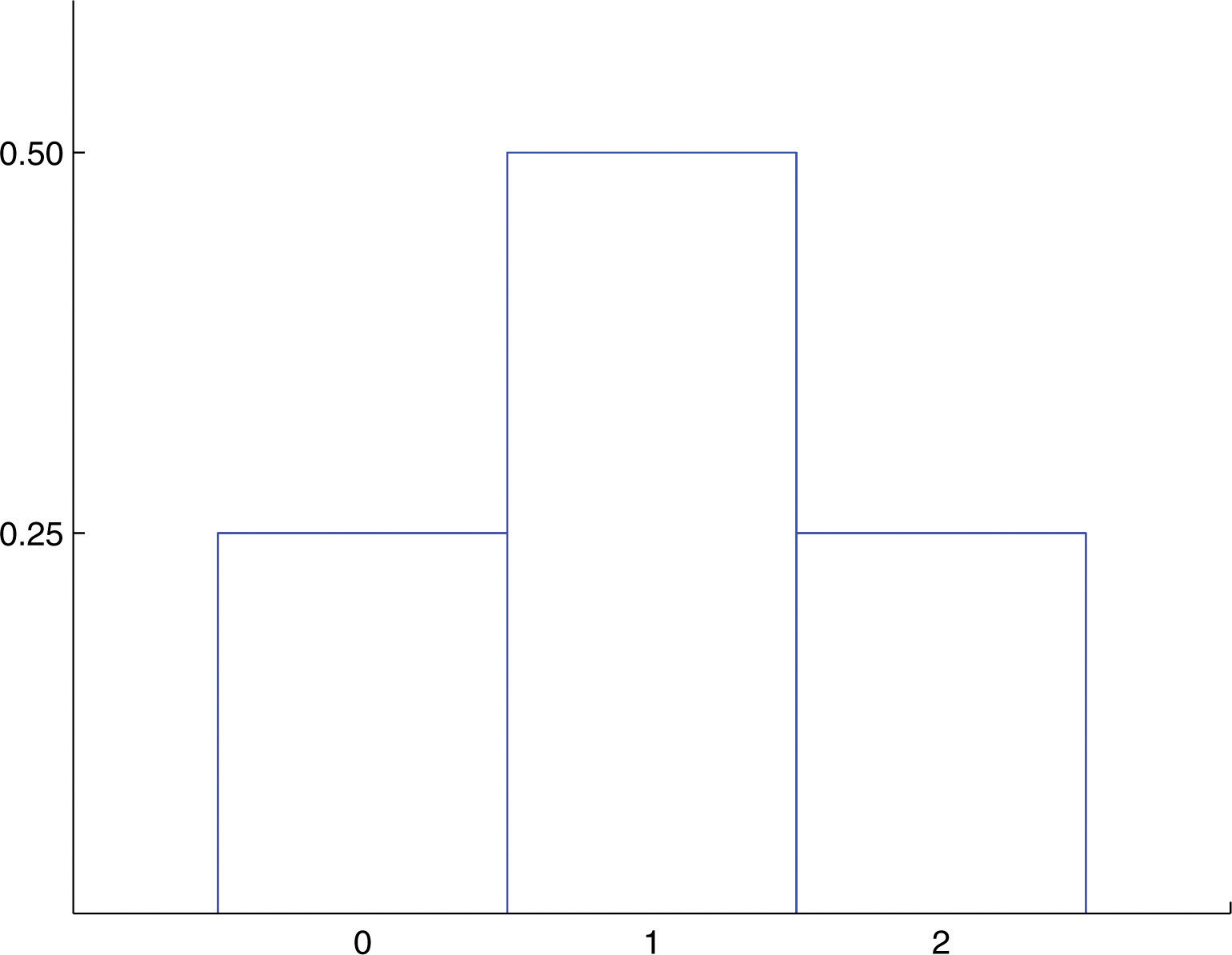
Example 2

A pair of off-white dice is rolled. Allow 10 denote the sum of the number of dots on the top faces.

1. Construct the probability distribution of 10.
2. Detect P(Ten ≥ nine).
3. Find the probability that 10 takes an even value.

Solution:

The sample space of equally probable outcomes is

$$\begin{array}{cccccc}\mathrm{xi}& 12& \mathrm{xiii}& \mathrm{fourteen}& \mathrm{xv}& \mathrm{xvi}\\ 21& 22& 23& 24& 25& 26\\ 31& 32& 33& 34& 35& 36\\ 41& 42& 43& 44& 45& 46\\ 51& 52& 53& 54& 55& 56\\ 61& 62& 63& 64& 65& 66\end{array}$$

1. The possible values for X are the numbers ii through 12. X = two is the outcome {11}, so $P\left(2\right)=\mathrm{ane}∕36.$ X = 3 is the consequence {12,21}, so $P\left(3\right)=2∕36.$ Standing this way we obtain the table

   $$\begin{array}{cccccccccccc}x& 2& 3& \mathrm{four}& 5& \mathrm{half\; dozen}& 7& 8& 9& 10& 11& 12\\ P\left(x\right)& \frac{\mathrm{i}}{36}& \frac{2}{36}& \frac{3}{36}& \frac{\mathrm{four}}{36}& \frac{5}{36}& \frac{\mathrm{vi}}{36}& \frac{\mathrm{five}}{36}& \frac{4}{36}& \frac{3}{36}& \frac{\mathrm{ii}}{36}& \frac{1}{36}\end{array}$$

   This table is the probability distribution of X.

2. The event X ≥ 9 is the union of the mutually exclusive events 10 = nine, 10 = 10, X = 11, and X = 12. Thus

   $$P\left(\mathrm{10}\ge 9\right)=P\left(\mathrm{nine}\right)+P\left(\mathrm{ten}\right)+P\left(11\right)+P\left(12\right)=\frac{4}{36}+\frac{3}{36}+\frac{2}{36}+\frac{1}{36}=\frac{10}{36}=\mathrm{0.two}\stackrel{-}{7}$$

3. Earlier we immediately jump to the determination that the probability that X takes an fifty-fifty value must be 0.5, notation that X takes six different fifty-fifty values only only five different odd values. We compute

   $$\begin{array}{lll}\hfill P\left(X\text{\hspace{0.17em}is\hspace{0.17em}even}\right)& =& P\left(2\right)+P\left(\mathrm{four}\right)+P\left(6\right)+P\left(8\right)+P\left(10\right)+P\left(12\right)\\ & =& \frac{\mathrm{ane}}{36}+\frac{3}{36}+\frac{5}{36}+\frac{5}{36}+\frac{3}{36}+\frac{1}{36}=\frac{18}{36}=\mathrm{0.five}\end{array}$$

   A histogram that graphically illustrates the probability distribution is given in Figure 4.2 "Probability Distribution for Tossing Ii Fair Dice".

Figure 4.2 Probability Distribution for Tossing Two Fair Dice

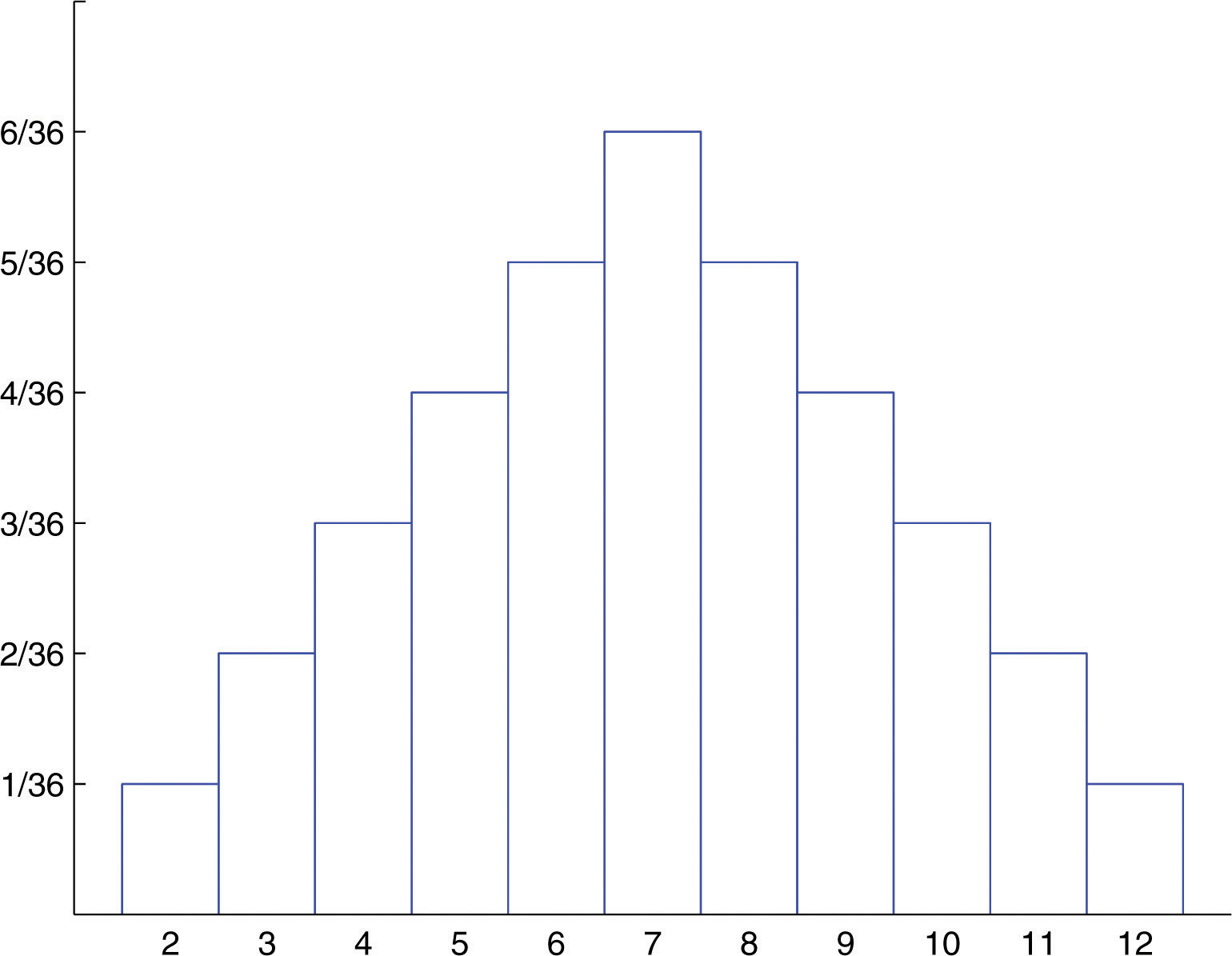
The Mean and Standard Deviation of a Discrete Random Variable

Definition

The hatefulThe number ${\displaystyle \mathrm{\Sigma }xP\left(x\right)}$ , measuring its boilerplate upon repeated trials. (also chosen the expected valueIts mean. ) of a detached random variable 10 is the number

$$\mathit{\mu }=E\left(X\right)=\mathrm{\Sigma }xP\left(x\right)$$

The hateful of a random variable may be interpreted every bit the average of the values causeless past the random variable in repeated trials of the experiment.

Case 3

Find the hateful of the discrete random variable 10 whose probability distribution is

$$\begin{array}{ccccc}x& \text{−}2& \mathrm{ane}& \mathrm{ii}& \mathrm{iii.5}\\ P\left(x\right)& 0.21& 0.34& 0.24& 0.21\end{array}$$

Solution:

The formula in the definition gives

$$\begin{array}{lll}\hfill \mathit{\mu }& =& \mathrm{\Sigma }\mathrm{ten}P\left(\mathrm{10}\right)\\ & =& \left(\text{−}2\right)·0.21+\left(1\right)·0.34+\left(2\right)·0.24+\left(\mathrm{three.5}\right)·0.21=\mathrm{ane.135}\end{array}$$

Instance 4

A service system in a large boondocks organizes a raffle each month. I yard raffle tickets are sold for $one each. Each has an equal chance of winning. Kickoff prize is $300, 2d prize is $200, and third prize is $100. Let X denote the cyberspace gain from the purchase of one ticket.

1. Construct the probability distribution of X.
2. Find the probability of winning any money in the buy of ane ticket.
3. Discover the expected value of X, and interpret its meaning.

Solution:

1. If a ticket is selected as the first prize winner, the net gain to the purchaser is the $300 prize less the $1 that was paid for the ticket, hence X = 300 − one = 299. There is one such ticket, so P(299) = 0.001. Applying the aforementioned "income minus outgo" principle to the second and third prize winners and to the 997 losing tickets yields the probability distribution:

   $$\begin{array}{ccccc}x& 299& 199& 99& \text{−}\mathrm{one}\\ P\left(\mathrm{ten}\right)& 0.001& 0.001& 0.001& 0.997\end{array}$$

2. Permit West announce the event that a ticket is selected to win one of the prizes. Using the table

   $$P\left(W\right)=P\left(299\right)+P\left(199\right)+P\left(99\right)=0.001+0.001+0.001=0.003$$

3. Using the formula in the definition of expected value,

   $$E\left(X\right)=299·0.001+199·0.001+99·0.001+\left(\text{−}\mathrm{ane}\right)·0.997=\text{−}0.4$$

   The negative value ways that i loses money on the average. In particular, if someone were to buy tickets repeatedly, then although he would win now and then, on boilerplate he would lose 40 cents per ticket purchased.

The concept of expected value is as well basic to the insurance manufacture, equally the following simplified case illustrates.

Example 5

A life insurance company volition sell a $200,000 one-year term life insurance policy to an individual in a particular risk grouping for a premium of $195. Find the expected value to the company of a single policy if a person in this gamble group has a 99.97% chance of surviving one yr.

Solution:

Let Ten denote the net gain to the company from the sale of one such policy. There are two possibilities: the insured person lives the whole year or the insured person dies earlier the year is upward. Applying the "income minus outgo" principle, in the former case the value of X is 195 − 0; in the latter example it is $195-\mathrm{200,000}=\text{−}\mathrm{199,805}.$ Since the probability in the first case is 0.9997 and in the 2d case is $1-0.9997=0.0003$ , the probability distribution for 10 is:

$$\begin{array}{ccc}x& 195& \text{−}\mathrm{199,805}\\ P\left(x\right)& 0.9997& 0.0003\end{array}$$

Therefore

$$\mathrm{East}\left(X\right)=\mathrm{\Sigma }xP\left(x\right)=195·0.9997+\left(\text{−}\mathrm{199,805}\right)·0.0003=135$$

Occasionally (in fact, 3 times in 10,000) the company loses a large amount of money on a policy, but typically information technology gains $195, which by our computation of $E\left(\mathrm{10}\right)$ works out to a net gain of $135 per policy sold, on average.

Definition

The variance, ${\mathit{\sigma }}^{\mathrm{two}}$ , of a discrete random variable X is the number

$${\mathit{\sigma }}^2=\mathrm{\Sigma }{\left(\mathrm{ten}-\mathit{\mu }\right)}^{2}P\left(x\right)$$

which by algebra is equivalent to the formula

$${\mathit{\sigma }}^2=\left[\right.\mathrm{\Sigma }{x}^{\mathrm{two}}P\left(\mathrm{ten}\right)\left]\right.-{\mathit{\mu }}^2$$

Definition

The standard departureThe number $\sqrt{{\displaystyle \mathrm{\Sigma }{(\mathrm{10}-\mathit{\mu })}^{\mathrm{ii}}P\left(\mathrm{10}\right)}}$ (also computed using $\sqrt{\left[{\displaystyle \mathrm{\Sigma }{\mathrm{10}}^{2}P\left(\mathrm{10}\right)}\right]-{\mathit{\mu }}^2}$ ), measuring its variability nether repeated trials. , σ, of a discrete random variable X is the square root of its variance, hence is given by the formulas

$$\mathit{\sigma }=\sqrt{\mathrm{\Sigma }{\left(x-\mathit{\mu }\right)}^{2}P\left(\mathrm{ten}\right)}=\sqrt{\left[\right.\mathrm{\Sigma }{x}^{2}P\left(x\right)\left]\right.-{\mathit{\mu }}^2}$$

The variance and standard deviation of a discrete random variable X may be interpreted equally measures of the variability of the values assumed by the random variable in repeated trials of the experiment. The units on the standard divergence friction match those of X.

Case 6

A discrete random variable X has the following probability distribution:

$$\begin{array}{ccccc}\mathrm{10}& \text{−}1& 0& \mathrm{i}& 4\\ P\left(\mathrm{10}\right)& 0.2& \mathrm{0.five}& a& 0.1\end{array}$$

A histogram that graphically illustrates the probability distribution is given in Figure 4.three "Probability Distribution of a Discrete Random Variable".

Figure 4.3 Probability Distribution of a Discrete Random Variable

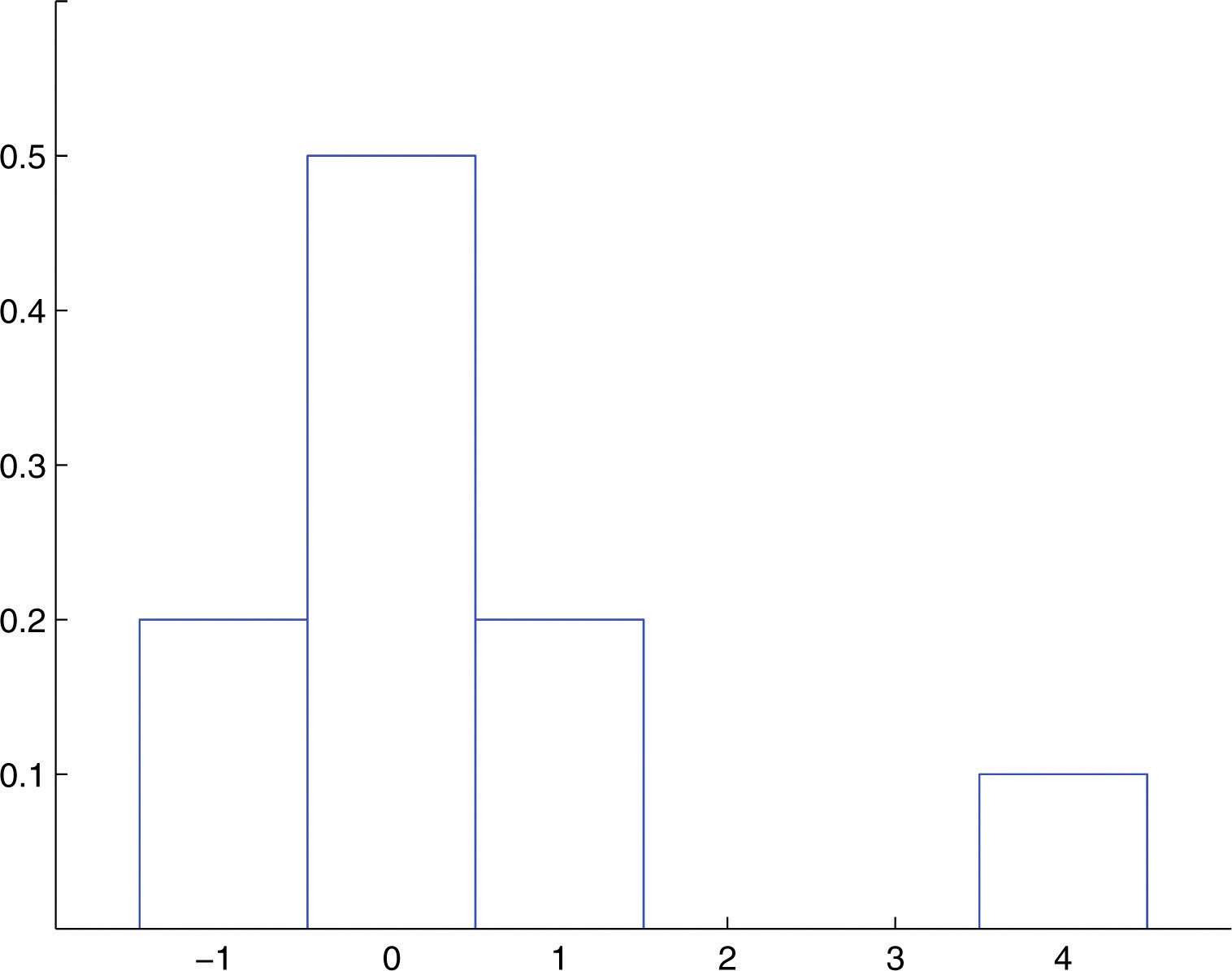
Compute each of the following quantities.

1. a.
2. $P\left(0\right).$
3. P(X > 0).
4. P(Ten ≥ 0).
5. $P\left(X\le \text{−}2\right).$
6. The mean μ of Ten.
7. The variance ${\mathit{\sigma }}^2$ of X.
8. The standard divergence σ of X.

Solution:

1. Since all probabilities must add up to i, $a=\mathrm{ane}-\left(0.2+0.5+0.1\right)=0.2.$
2. Direct from the table, $P\left(0\right)=0.5.$
3. From the tabular array, $P\left(\mathrm{10}>0\right)=P\left(1\right)+P\left(4\right)=0.2+0.1=0.3.$
4. From the table, $P\left(X\ge 0\right)=P\left(0\right)+P\left(1\right)+P\left(4\right)=\mathrm{0.five}+0.2+0.1=\mathrm{0.viii}.$
5. Since none of the numbers listed as possible values for Ten is less than or equal to −2, the event X ≤ −two is impossible, so P(X ≤ −2) = 0.

6. Using the formula in the definition of μ,

   $$\mathit{\mu }=\mathrm{\Sigma }\mathrm{ten}P\left(\mathrm{10}\right)=\left(\text{−}1\right)·0.2+0·0.5+1·\mathrm{0.two}+4·\mathrm{0.i}=0.4$$

7. Using the formula in the definition of ${\mathit{\sigma }}^2$ and the value of μ that was just computed,

   $$\begin{array}{lll}\hfill {\mathit{\sigma }}^2& =& \mathrm{\Sigma }{\left(x-\mathit{\mu }\right)}^{\mathrm{two}}P\left(x\right)\\ & =& {\left(\text{−}1-\mathrm{0.iv}\right)}^{\mathrm{two}}·0.2+{\left(0-\mathrm{0.four}\right)}^2·0.5+{\left(1-0.4\right)}^{\mathrm{ii}}·0.2+{\left(\mathrm{iv}-0.4\right)}^2·\mathrm{0.one}\\ & =& \mathrm{ane.84}\end{array}$$
8. Using the result of function (chiliad), $\mathit{\sigma }=\sqrt{1.84}=\mathrm{one.3565}.$

Key Takeaways

• The probability distribution of a discrete random variable X is a list of each possible value x taken past Ten along with the probability $P\left(\mathrm{10}\right)$ that X takes that value in one trial of the experiment.
• The mean μ of a discrete random variable Ten is a number that indicates the average value of X over numerous trials of the experiment. It is computed using the formula $\mathit{\mu }={\displaystyle \mathrm{\Sigma }xP\left(\mathrm{10}\right)}.$
• The variance ${\mathit{\sigma }}^{\mathrm{ii}}$ and standard deviation σ of a discrete random variable X are numbers that signal the variability of Ten over numerous trials of the experiment. They may be computed using the formula ${\mathit{\sigma }}^2=\left[{\displaystyle \mathrm{\Sigma }{x}^2}P\left(x\right)\right]-{\mathit{\mu }}^2$ , taking the foursquare root to obtain σ.

Exercises

Bones

1. Determine whether or non the table is a valid probability distribution of a discrete random variable. Explain fully.

   1. $\begin{array}{ccccc}x& \text{−}2& 0& 2& \mathrm{iv}\\ P\left(x\right)& 0.3& 0.5& \mathrm{0.ii}& \mathrm{0.one}\end{array}$

   2. $\begin{array}{cccc}x& 0.5& 0.25& 0.25\\ P\left(x\right)& \text{−}\mathrm{0.iv}& 0.6& 0.8\end{array}$

   3. $\begin{array}{cccccc}\mathrm{ten}& 1.1& 2.5& 4.1& \mathrm{four.half-dozen}& \mathrm{5.three}\\ P\left(\mathrm{10}\right)& \mathrm{0.xvi}& 0.14& 0.11& 0.27& 0.22\end{array}$

2. Determine whether or not the tabular array is a valid probability distribution of a discrete random variable. Explicate fully.

   1. $\begin{array}{cccccc}\mathrm{ten}& 0& 1& 2& \mathrm{iii}& 4\\ P\left(x\right)& \text{−}0.25& \mathrm{0.fifty}& 0.35& \mathrm{0.ten}& 0.30\end{array}$

   2. $\begin{array}{cccc}x& 1& \mathrm{two}& \mathrm{three}\\ P\left(x\right)& 0.325& 0.406& 0.164\end{array}$

   3. $\begin{array}{cccccc}x& 25& 26& 27& 28& 29\\ P\left(\mathrm{10}\right)& 0.13& 0.27& 0.28& \mathrm{0.eighteen}& \mathrm{0.fourteen}\end{array}$

3. A detached random variable 10 has the following probability distribution:

   $$\begin{array}{cccccc}\mathrm{10}& 77& 78& 79& 80& 81\\ P\left(x\right)& 0.15& \mathrm{0.fifteen}& \mathrm{0.xx}& \mathrm{0.forty}& 0.10\end{array}$$

   Compute each of the following quantities.

   1. $P\left(80\right).$
   2. P(X > 80).
   3. P(Ten ≤ 80).
   4. The mean μ of Ten.
   5. The variance ${\mathit{\sigma }}^2$ of X.
   6. The standard divergence σ of X.

4. A discrete random variable X has the following probability distribution:

   $$\begin{array}{cccccc}x& \mathrm{thirteen}& 18& 20& 24& 27\\ P\left(x\right)& 0.22& 0.25& 0.20& 0.17& 0.16\end{array}$$

   Compute each of the following quantities.

   1. $P\left(18\right).$
   2. P(X > 18).
   3. P(X ≤ 18).
   4. The mean μ of 10.
   5. The variance ${\mathit{\sigma }}^{\mathrm{two}}$ of 10.
   6. The standard deviation σ of 10.

5. If each die in a pair is "loaded" so that one comes up half equally often as it should, six comes up half again every bit often as it should, and the probabilities of the other faces are unaltered, then the probability distribution for the sum X of the number of dots on the peak faces when the 2 are rolled is

   $$\begin{array}{ccccccc}x& 2& 3& 4& 5& 6& \mathrm{seven}\\ P\left(x\right)& \frac{\mathrm{one}}{144}& \frac{4}{144}& \frac{8}{144}& \frac{12}{144}& \frac{16}{144}& \frac{22}{144}\end{array}$$ $$\begin{array}{cccccc}\mathrm{ten}& \mathrm{viii}& \mathrm{ix}& 10& 11& 12\\ P\left(x\right)& \frac{24}{144}& \frac{\mathrm{xx}}{144}& \frac{\mathrm{xvi}}{144}& \frac{12}{144}& \frac{\mathrm{ix}}{144}\end{array}$$

   Compute each of the following.

   1. $P\left(\mathrm{v}\le \mathrm{10}\le 9\right).$
   2. P(X ≥ 7).
   3. The mean μ of X. (For fair dice this number is 7.)
   4. The standard deviation σ of X. (For fair dice this number is almost 2.415.)

Applications

6. Borachio works in an automotive tire factory. The number 10 of sound only blemished tires that he produces on a random solar day has the probability distribution

   $$\begin{array}{ccccc}x& 2& 3& 4& \mathrm{five}\\ P\left(x\right)& 0.48& 0.36& 0.12& 0.04\end{array}$$

   1. Find the probability that Borachio will produce more than iii blemished tires tomorrow.
   2. Observe the probability that Borachio volition produce at near 2 blemished tires tomorrow.
   3. Compute the mean and standard divergence of X. Interpret the mean in the context of the problem.

7. In a hamster breeder'southward experience the number X of live pups in a litter of a female person not over twelve months in age who has not borne a litter in the by vi weeks has the probability distribution

   $$\begin{array}{cccccccc}x& 3& 4& 5& 6& 7& \mathrm{viii}& 9\\ P\left(x\right)& 0.04& 0.10& 0.26& 0.31& 0.22& 0.05& 0.02\end{array}$$

   1. Find the probability that the adjacent litter will produce five to vii live pups.
   2. Find the probability that the adjacent litter volition produce at to the lowest degree six live pups.
   3. Compute the hateful and standard deviation of X. Translate the mean in the context of the problem.

8. The number X of days in the summertime months that a construction crew cannot work considering of the weather has the probability distribution

   $$\begin{array}{cccccc}x& 6& 7& 8& \mathrm{nine}& 10\\ P\left(x\right)& 0.03& 0.08& 0.15& 0.20& \mathrm{0.nineteen}\end{array}$$ $$\begin{array}{ccccc}\mathrm{10}& 11& 12& \mathrm{thirteen}& \mathrm{xiv}\\ P\left(\mathrm{10}\right)& \mathrm{0.sixteen}& \mathrm{0.ten}& 0.07& 0.02\end{array}$$

   1. Detect the probability that no more than ten days will be lost next summer.
   2. Discover the probability that from viii to 12 days will exist lost next summertime.
   3. Find the probability that no days at all will exist lost next summer.
   4. Compute the mean and standard departure of X. Interpret the mean in the context of the problem.

9. Let X announce the number of boys in a randomly selected 3-child family. Assuming that boys and girls are equally likely, construct the probability distribution of X.

10. Let Ten announce the number of times a fair money lands heads in three tosses. Construct the probability distribution of X.

11. Five m lottery tickets are sold for $1 each. Ane ticket volition win $1,000, two tickets will win $500 each, and 10 tickets will win $100 each. Let 10 denote the net gain from the purchase of a randomly selected ticket.

    1. Construct the probability distribution of Ten.
    2. Compute the expected value $E\left(X\right)$ of X. Translate its pregnant.
    3. Compute the standard deviation σ of X.

12. 7 chiliad lottery tickets are sold for $v each. One ticket will win $2,000, two tickets will win $750 each, and five tickets will win $100 each. Permit 10 denote the net proceeds from the purchase of a randomly selected ticket.

    1. Construct the probability distribution of X.
    2. Compute the expected value $E\left(X\right)$ of 10. Interpret its meaning.
    3. Compute the standard deviation σ of X.

13. An insurance company will sell a $90,000 one-year term life insurance policy to an individual in a detail take a chance group for a premium of $478. Find the expected value to the visitor of a single policy if a person in this risk group has a 99.62% chance of surviving ane year.

14. An insurance company will sell a $10,000 one-year term life insurance policy to an private in a particular run a risk group for a premium of $368. Find the expected value to the company of a single policy if a person in this risk grouping has a 97.25% chance of surviving i yr.

15. An insurance company estimates that the probability that an private in a particular hazard group will survive one year is 0.9825. Such a person wishes to purchase a $150,000 one-year term life insurance policy. Allow C denote how much the insurance company charges such a person for such a policy.

    1. Construct the probability distribution of Ten. (Two entries in the tabular array will contain C.)
    2. Compute the expected value $E\left(X\right)$ of 10.
    3. Determine the value C must have in social club for the company to break even on all such policies (that is, to average a net gain of nix per policy on such policies).
    4. Determine the value C must have in order for the company to average a net proceeds of $250 per policy on all such policies.

16. An insurance company estimates that the probability that an individual in a item run a risk group will survive one year is 0.99. Such a person wishes to buy a $75,000 one-year term life insurance policy. Let C denote how much the insurance company charges such a person for such a policy.

    1. Construct the probability distribution of X. (Two entries in the tabular array will contain C.)
    2. Compute the expected value $E\left(\mathrm{10}\right)$ of X.
    3. Determine the value C must have in lodge for the visitor to intermission even on all such policies (that is, to average a net proceeds of goose egg per policy on such policies).
    4. Determine the value C must have in guild for the company to average a net gain of $150 per policy on all such policies.

17. A roulette bicycle has 38 slots. 30-6 slots are numbered from 1 to 36; half of them are cherry-red and half are blackness. The remaining two slots are numbered 0 and 00 and are green. In a $ane bet on cherry, the bettor pays $1 to play. If the brawl lands in a red slot, he receives dorsum the dollar he bet plus an additional dollar. If the ball does not land on red he loses his dollar. Permit X announce the net gain to the bettor on one play of the game.

    1. Construct the probability distribution of Ten.
    2. Compute the expected value $E\left(X\right)$ of X, and translate its meaning in the context of the trouble.
    3. Compute the standard departure of X.

18. A roulette cycle has 38 slots. 30-six slots are numbered from 1 to 36; the remaining two slots are numbered 0 and 00. Suppose the "number" 00 is considered not to be even, but the number 0 is still even. In a $1 bet on fifty-fifty, the bettor pays $1 to play. If the ball lands in an even numbered slot, he receives back the dollar he bet plus an boosted dollar. If the ball does not country on an even numbered slot, he loses his dollar. Let X denote the internet proceeds to the bettor on one play of the game.

    1. Construct the probability distribution of X.
    2. Compute the expected value $E\left(\mathrm{Ten}\right)$ of 10, and explain why this game is not offered in a casino (where 0 is not considered even).
    3. Compute the standard divergence of Ten.

19. The fourth dimension, to the nearest whole minute, that a city double-decker takes to go from one cease of its road to the other has the probability distribution shown. As sometimes happens with probabilities computed as empirical relative frequencies, probabilities in the table add together up but to a value other than i.00 because of round-off error.

    $$\begin{array}{ccccccc}x& 42& 43& 44& 45& 46& 47\\ P\left(\mathrm{ten}\right)& 0.10& 0.23& 0.34& 0.25& 0.05& 0.02\end{array}$$

    1. Detect the average time the bus takes to drive the length of its route.
    2. Find the standard deviation of the length of time the autobus takes to drive the length of its road.

20. Tybalt receives in the mail an offer to enter a national sweepstakes. The prizes and chances of winning are listed in the offer as: $5 million, ane chance in 65 one thousand thousand; $150,000, one chance in 6.5 meg; $5,000, i chance in 650,000; and $1,000, one chance in 65,000. If it costs Tybalt 44 cents to post his entry, what is the expected value of the sweepstakes to him?

Additional Exercises

21. The number Ten of nails in a randomly selected 1-pound box has the probability distribution shown. Find the boilerplate number of nails per pound.

    $$\begin{array}{cccc}x& 100& 101& 102\\ P\left(x\right)& 0.01& 0.96& 0.03\end{array}$$

22. Three fair dice are rolled at once. Let 10 denote the number of die that country with the aforementioned number of dots on top equally at least one other die. The probability distribution for X is

    $$\begin{array}{cccc}x& 0& u& 3\\ P\left(x\right)& p& \frac{\mathrm{xv}}{36}& \frac{1}{36}\end{array}$$

    1. Observe the missing value u of X.
    2. Notice the missing probability p.
    3. Compute the hateful of Ten.
    4. Compute the standard deviation of X.

23. Two fair dice are rolled at once. Allow X denote the difference in the number of dots that appear on the acme faces of the two dice. Thus for example if a one and a five are rolled, Ten = 4, and if two sixes are rolled, X = 0.

    1. Construct the probability distribution for Ten.
    2. Compute the mean μ of X.
    3. Compute the standard deviation σ of X.

24. A fair coin is tossed repeatedly until either it lands heads or a total of 5 tosses have been made, whichever comes first. Let X announce the number of tosses fabricated.

    1. Construct the probability distribution for X.
    2. Compute the hateful μ of X.
    3. Compute the standard deviation σ of X.

25. A manufacturer receives a sure component from a supplier in shipments of 100 units. Ii units in each shipment are selected at random and tested. If either one of the units is defective the shipment is rejected. Suppose a shipment has 5 lacking units.

    1. Construct the probability distribution for the number X of defective units in such a sample. (A tree diagram is helpful.)
    2. Discover the probability that such a shipment volition be accepted.

26. Shylock enters a local co-operative banking concern at 4:xxx p.m. every payday, at which time there are always two tellers on duty. The number X of customers in the bank who are either at a teller window or are waiting in a single line for the next bachelor teller has the following probability distribution.

    $$\begin{array}{ccccc}x& 0& 1& 2& \mathrm{three}\\ P\left(x\right)& 0.135& 0.192& 0.284& 0.230\end{array}$$ $$\begin{array}{cccc}x& 4& 5& 6\\ P\left(x\right)& 0.103& 0.051& 0.005\end{array}$$

    1. What number of customers does Shylock most often encounter in the bank the moment he enters?
    2. What number of customers waiting in line does Shylock most often encounter the moment he enters?
    3. What is the average number of customers who are waiting in line the moment Shylock enters?

27. The possessor of a proposed outdoor theater must determine whether to include a encompass that will allow shows to be performed in all weather condition weather. Based on projected audience sizes and weather conditions, the probability distribution for the revenue X per night if the comprehend is not installed is

    $$\begin{array}{lll}\text{Weather condition}\hfill & \hfill x\hfill & \hfill P\left(x\right)\hfill \\ \text{Clear}\hfill & \hfill \text{\$3000}\hfill & \hfill \text{0}\text{.61}\hfill \\ \text{Threatening}\hfill & \hfill \text{\$2800}\hfill & \hfill \text{0}\text{.17}\hfill \\ \text{Lite\hspace{0.17em}rain}\hfill & \hfill \text{\$1975}\hfill & \hfill \text{0}\text{.eleven}\hfill \\ \text{Show-cancelling\hspace{0.17em}rain}\hfill & \hfill \text{\$0}\hfill & \hfill \text{0}\text{.11}\hfill \end{array}$$

    The additional price of the cover is $410,000. The owner will have it built if this cost tin can exist recovered from the increased revenue the cover affords in the first x 90-night seasons.

    1. Compute the mean revenue per night if the encompass is non installed.
    2. Utilize the answer to (a) to compute the projected total revenue per 90-night season if the comprehend is not installed.
    3. Compute the projected total revenue per season when the cover is in place. To do so presume that if the comprehend were in place the revenue each night of the season would exist the same as the revenue on a clear night.
    4. Using the answers to (b) and (c), decide whether or non the additional cost of the installation of the embrace will exist recovered from the increased revenue over the get-go x years. Will the owner have the embrace installed?

Answers

1. 1. no: the sum of the probabilities exceeds 1
   2. no: a negative probability
   3. no: the sum of the probabilities is less than 1
3. 1. 0.4
   2. 0.1
   3. 0.9
   4. 79.15
   5. ${\mathit{\sigma }}^2=1.5275$
   6. σ = 1.2359
5. 1. 0.6528
   2. 0.7153
   3. μ = 7.8333
   4. ${\mathit{\sigma }}^{\mathrm{two}}=5.4866$
   5. σ = two.3424

7. 1. 0.79
   2. 0.60
   3. μ = 5.8, σ = i.2570

11. 1. $\begin{array}{ccccc}\mathrm{10}& \text{−}1& 999& 499& 99\\ P\left(x\right)& \frac{4987}{5000}& \frac{1}{5000}& \frac{2}{5000}& \frac{10}{5000}\end{array}$

    2. −0.iv
    3. 17.8785

13. 136

15. 1. $\begin{array}{ccc}x& C& C\text{−}\mathrm{150,000}\\ P\left(x\right)& 0.9825& 0.0175\end{array}$

    2. $C\text{−}2625$
    3. C ≥ 2625
    4. C ≥ 2875

17. 1. $\begin{array}{ccc}\mathrm{ten}& \text{−}1& 1\\ P\left(\mathrm{10}\right)& \frac{20}{38}& \frac{18}{38}\end{array}$

    2. $E\left(X\right)=\text{−}0.0526$ In many bets the bettor sustains an average loss of nigh 5.25 cents per bet.
    3. 0.9986
19. 1. 43.54
    2. one.2046

21. 101.02

23. 1. $\begin{array}{ccccccc}x& 0& 1& 2& 3& \mathrm{iv}& 5\\ P\left(x\right)& \frac{\mathrm{half\; dozen}}{36}& \frac{\mathrm{ten}}{36}& \frac{8}{36}& \frac{6}{36}& \frac{4}{36}& \frac{\mathrm{ii}}{36}\end{array}$

    2. ane.9444
    3. 1.4326

25. 1. $\begin{array}{cccc}x& 0& 1& 2\\ P\left(x\right)& 0.902& 0.096& 0.002\end{array}$

    2. 0.902
27. 1. 2523.25
    2. 227,092.5
    3. 270,000
    4. The owner will install the embrace.

adamsjoacity.blogspot.com

Source: https://saylordotorg.github.io/text_introductory-statistics/s08-02-probability-distributions-for-.html

Share this post